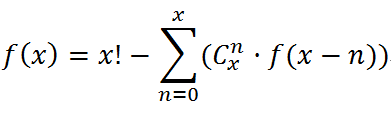最近被问到了这么一个问题,蛮有意思的. 这里可以做一个额外的限定:在有限的步骤内精确地将发生的事件分割成六个概率为 1/6 的部分,而不是随着操作次数的次数增多趋近 1/6.
经过了一段时间的探索之后,我发现想要通过重复掷固定次数的骰子来达成这一目标,在知道六面各自的概率后,是不存在一个策略可以把所有发生的事件精确地分割成六份的.
我将借助超越数,使用反证法来证明这一点.
为了证明这一点,首先可以做一些化简. 六面的骰子过于复杂,可以先尝试减少到两面,也就是把骰子简化成硬币. 假设这样的策略是存在的,也就是给定一个六面概率不一的骰子及其各面概率后,就可以得到一个正整数 n,然后掷这个骰子 n 次,根据每次掷的结果将结果分为等概率的六份. 然后假设存在一种只有两面的各面概率不一的骰子.
首先,这个两面骰子可以做到六面骰子的效果. 方法是掷三次两面骰子,可以得到八种不同的结果,将这八种结果分为六份(不能有任何一份是空的),就可以得到六个概率不一的事件集. 而根据刚才的假设,知道了六种结果的概率后,把它当作一个六面的骰子,重复 n 次掷骰子的操作,然后就可以得到均匀概率的六组结果. 最后,将这六种结果的其中三种分为一组,另三组分为一组,这样就得到了均匀概率的两组结果. 也就是说,当六面骰子的策略存在的时候,两面骰子的策略也同样存在.

 (图片来源:
(图片来源: